In order to determine the relative merits of the various solar panel types we must examine the differences in capabilities between these types of panels. The methodology of this process will use data collected from the “real world” specifications and qualitative description of solar panels available for purchase at the time of this review. While the efficiency and possible cost of cutting edge technology presented in academic papers will certainly be better than what this review will find this technology will still be confined to laboratories and small scale tests. This is unsuitable for our application where panels that are easily sourced and have “backup” secondary sources are necessary. We will use the Topoint 245W JTM 250-96M Solar Panel, Topoint 225W JTM225-60P Solar Panel, and Uni-Solar Laminate 136 Watt PVL-136 as references as research has shown they seen to be reasonably representative of what is available. We can use their product specifications to determine some figures of merit for comparison purposes.
Solar Panel Specifications
| Panel | Max Power at STC (W) | Size (m2) |
| Topoint 245W JTM 250-96M Solar Panel, Mono | 245 | 1.704 |
| Topoint 225W JTM225-60P Solar Panel, Poly | 225 | 1.636 |
| Uni-Solar Laminate 136 Watt PVL-136, Thin Film | 136 | 2.160 |
The following figures of merit are used to compare important characteristics of each panel type. These values are derived from the specifications in the above table. All figures are based on the panel performance at STC.
- Cost per Watt: This figure determines how costly it is to supply each Watt of power. Lower is better.
- Power Gathered: This metric shows how much power each square meter of panel is expected to gather per square meter. Higher is better.
Solar Panel Figures of Merit
| Panel Type | Cost Per Watt ($/W) | Power Gathered (W/m2) |
| Monocrystalline | .78 | 143.77 |
| Polycrystalline | .62 | 137.53 |
| Thin Film | .47 | 62.96 |
The dollars per Watt ($/W) metric shows how efficient panels are in terms of their cost per amount of power delivered. This metric takes into account the efficiency a panel has when converting light to electricity as well as the cost of the technology. The Watts per square meter (W/m2 ) metric show how space efficient panels are. This can help determine the space required for a given panel for a certain delivered power.
These figures of merit show that Monocrystalline panels are the most efficient in terms of how much power they provide per amount of space they take up. This is offset by their high cost. Polycrystalline panels are a close second showing that in all but the most space conscious applications polycrystalline is superior to monocrystalline. Trailing far behind in space efficiency are solar generator with solar panels. These are very inefficient in terms of space but are very cheap, even when factoring in their inefficiency. Thin film technology has another benefit not shown in these tables. The ability to flex, fold, and even be rolled up is a material property which other more efficient panels do not have. This can be very useful when designing products. Portability, ruggedness, integration into textiles, and other “real world” factors are improved by using flexible panels. To some extent mono- and polycrystalline panels can be made to be slightly flexible, but this somewhat impacts their efficiency and these panels do not flex nearly as much as true thin film panels.
To extend our analysis further we must examine our application more closely. Typical laptops (excluding the uncommon power hungry “gaming” laptops and similar) will draw about 60W when in use and charging the battery. Mobile phones will consume about 6W when charging. If we use the assumption that two laptops and four cell phones are charging at once we get a total power draw of 144W. If we assume that converting the DC power from the generator with solar panels to 5v DC and 120v AC will have approximately 80% efficiency the total draw is 180W.Solar generator specifications are tested under “STC”, Standard Test Conditions, which is a set of standards including the assumption of 1000W/m2 energy from the sun. This is close to the maximum amount delivered to the earth. A more typical amount of energy is around 500W/m2 . Thus the panels must be rated at 360W total to deliver 180W under typical conditions. This is the amount of power a Solar Charging Station will need from the solar panels and battery backup under “worst case” conditions.
We can use this number to determine some more specific info about the cost and size of the solar panels needed.
| Panel Type | Cost ($) | Size (m2) | Diameter of a Circle of the Required Size (m) |
| Monocrystalline | 280.80 | 2.5 | 1.8 |
| Polycrystalline | 223.20 | 2.6 | 1.8 |
| Thin Film | 169.20 | 5.7 | 2.7 |
Patio umbrellas are typically 9 to 12 feet (2.7m to 3.6m) in diameter. This range is large enough for all three common panel types to provide the necessary power. This means that when it comes to power generation all panel types are viable for use. With this in mind we must consider other avenues of differentiation between the panel types. The first is cost: thin film panels are the cheapest of the three panel technologies. The second is the physical and mechanical properties of the panel technologies. The thin film technology has the obvious advantage here with its flexibility allowing it to more easily conform to the existing umbrella fabric. Ease of use will be important with this product. The more closely the operation of this charging station mimics that of a traditional patio umbrella the more likely it is to be a viable product. With these attributes in mind it is clear that thin film technology is the most useful panel type for this application.
Modelling of Solar Cell
A photovoltaic solar cell is a complex device whose electrical properties that cannot be reduced to one single component such as an ideal voltage or current source. The physical realities of the solar cell necessitate a more complex understanding of the device. Thus in order to describe and simulate the properties of a solar cell one must build up a model which behaves in a similar way. A solar cell at its most basic has current source properties as it operates by using light to forcefully separate a set amount of charge. Furthermore, when short circuited a solar cell will produce a certain Isc which is characteristic of the cell at a particular light level. Thus at the center of our model is a current source. In addition to the Isc the solar cell has a certain Voc which is the voltage measured across its terminals when they are open circuited. We can model this behavior by placing a component in shunt with the current source. In addition to these components there are losses in the system which we can model as series and shunt resistances. This model is shown below.
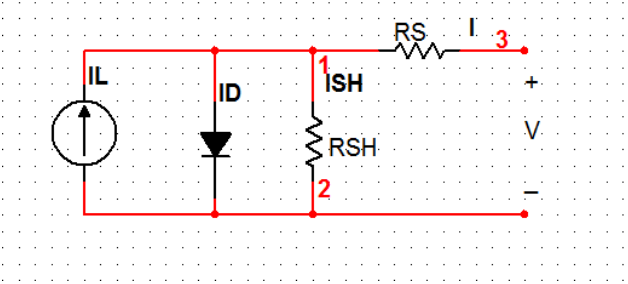
Here we see that the total current flowing out of the cell can be calculated by the following formula
𝐼 = 𝐼𝐿 − 𝐼𝐷 − 𝐼𝑆𝐻
Where IL is the current generated from the incident light, ID is the current flowing through the equivalent diode of the junction, and ISH is the current wasted in RSH.
The output voltage from this device can be found through the following equation where VJ is the voltage at node 1.
𝑉 = 𝑉𝐽 − 𝐼𝑅𝑆
In these equations the current ID is found through the standard Shockley diode equation. With these parameters this circuit can be fully simulated and characterized. It should be noted that due to the presence of the diode this is a transcendental equation which makes hand simulation difficult, as there are no analytical solutions to solving these equations. Fortunately the equations are simple and are easily simulated on a computer.
